An Intro To PathInterpolatorCompat
Version 22.1 of the v4 support library added several new Interpolator classes to help developers infuse their applications with Authentic Motion. Today, we’ll explore the highly-flexible PathInterpolatorCompat class.
As the name suggests, PathInterpolatorCompat is a utility for creating Path-based interpolators. The goals for this post are as follows:
- recap
Pathbasics; - understand which Paths can be used to create interpolators;
- understand the role of
PathInterpolatorCompatin the Android ecosystem; - build a
Path-based interpolator.
Paths
If it’s been a while since you worked with a Path, here’s the snappy definition from the docs:
The Path class encapsulates compound (multiple contour) geometric paths consisting of straight line segments, quadratic curves, and cubic curves.
In plainer English:
A Path is a collection of (not-necessarily-connected) straight lines, curves and shapes.
Paths are most commonly used to draw complex shapes on a Canvas via the Canvas.drawPath method. We build them by calling a sequence of methods to add new components. Key methods include but are not limited to:
Path.moveTo: sets the start point for the next contour.Path.lineTo: adds a straight line.Path.quadTo/Path.cubicTo: adds a quadratic/cubic bezier curve.Path.addArc/Path.addCircle/Path.addOval/Path.addRect: adds a shape with the specified geometry.
Here’s a super-simple example Path defined inside a custom view:
final Path path = new Path();
path.moveTo(0, getHeight());
path.lineTo(getWidth(), 0);This Path consists of a single straight line that starts at the bottom left corner of the view and ends at the top right corner of the view:

Here’s a more complex Path that consists of multiple components:
final Path path = new Path();
path.addCircle(
getWidth() / 2,
getHeight() / 2,
2 * getWidth() / 7,
Direction.CW
);
path.addCircle(
2 * getWidth() / 5,
3 * getHeight() / 7,
3 * pathPaint.getStrokeWidth(),
Direction.CW
);
path.addCircle(
3 * getWidth() / 5,
3 * getHeight() / 7,
3 * pathPaint.getStrokeWidth(),
Direction.CW
);
path.addArc(
new RectF(
getWidth() / 2 - 2 * getWidth() / 7,
getHeight() / 2 - 3 * getWidth() / 7,
getWidth() / 2 + 2 * getWidth() / 7,
getHeight() / 2 + getWidth() / 7
),
45,
90
);and the corresponding output:

Hopefully it’s clear that we can make super-general graphics using Path. However, this also means that we shouldn’t expect to be able to convert every Path into a valid interpolator. To figure out the appropriate constraints, let’s take a peek at some Android source code.
Interpolators ↔ Functions
The (abbreviated) source code for the TimeInterpolator interface below explains that an Android interpolator is nothing more than a function mapping the closed interval $[0,1]$ to the real numbers $\mathbb{R}$:
public interface TimeInterpolator {
/**
* [...]
*
* @param input A value between 0 and 1.0 indicating our current point
* in the animation where 0 represents the start and 1.0
* represents the end
* @return The interpolation value. This value can be more than 1.0
* for interpolators which overshoot their targets, or less
* than 0 for interpolators that undershoot their targets.
*/
float getInterpolation(float input);
}Armed with this context, the wordy restrictions placed on Paths passed as arguments to the PathInterpolator(Path path) and PathInterpolatorCompat(Path path) constructors become a little less mysterious - we just have to make sure our Path corresponds to the graph of some function $f$ satisfying $f(0) = 0$ and $f(1) = 1$.1
Function Representations
In general, a function $g(x)$ can be represented in one of three ways:
- algebraically:
- numerically:
| $x$ | $g(x)$ |
|---|---|
| $0$ | $0$ |
| $\frac{1}{4}$ | $\frac{1}{16}$ |
| $\frac{1}{2}$ | $\frac{1}{4}$ |
| $\frac{3}{4}$ | $\frac{9}{16}$ |
| $1$ | $1$ |
- graphically:
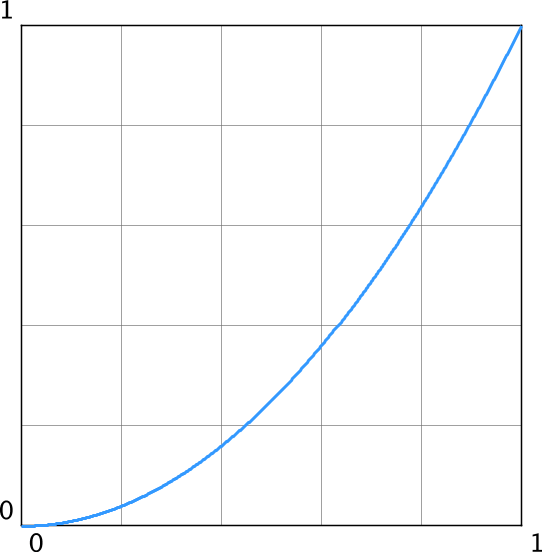
Prior to the release of Lollipop, all stock and most custom interpolators were defined algebraically. Framework examples include the ubiqituous AccelerateInterpolator:
public float getInterpolation(float input) {
if (mFactor == 1.0f) {
return input * input;
} else {
return (float)Math.pow(input, mDoubleFactor);
}
}and the quirky OvershootInterpolator2:
public float getInterpolation(float t) {
t -= 1.0f;
return t * t * ((mTension + 1) * t + mTension) + 1.0f;
}There are a couple of notable advantages to algebraic representations of interpolators:
-
they can be extremely compact;
-
physical motion (e.g. projectile, spring) can be modeled easily, because algebraic descriptions of motion are generally available.
However, there are also some significant drawbacks:
-
they can be extremely verbose (for e.g. piecewise-defined interpolators);
-
creating expressions that satisfy the boundary conditions is non-trivial; matching the desired high-level interpolator behavior too is very difficult indeed. This limitation makes it difficult to effectively explore the space of available interpolators.
PathInterpolatorCompat addresses the limitations above by allowing us first to design our interpolator graphically (an intuitive method, since most interpolators are used to generate animations), and then to represent this interpolator in code using the “natural language” methods provided by the Path class.
Using PathInterpolatorCompat
Great; we’ve figured out why PathInterpolatorCompat exists and which Paths we can convert into interpolators. Let’s give it a spin.
Our aim will be to construct a zig-zag interpolator whose interpolated value bounces between 0 and 1 $n$ times (where $n$ is odd). Here’s a graph that represents this zig-zag interpolator with $n=5$:
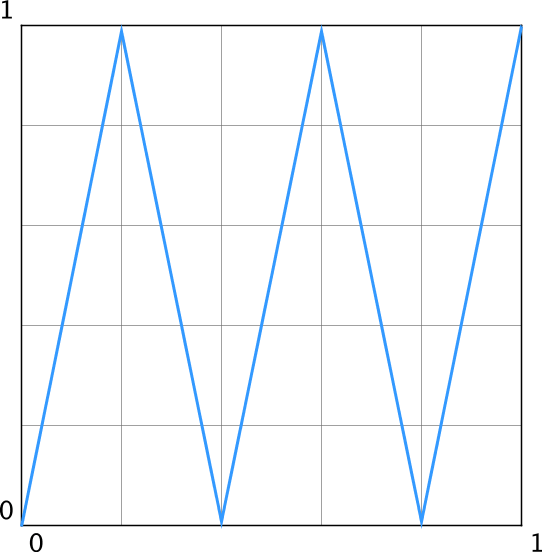
I’m not saying this is the most useful interpolator ever; I designed it to convince you that there exist interpolators that are more naturally represented by composite paths than by a single algebraic expression.
Here’s a Path-based representation of the class of interpolators described above:
final Path path = new Path();
final double n = 5;
for (int i = 1; i <= n; i++) {
path.lineTo(i / n, i % 2);
}
final TimeInterpolator result = new PathInterpolatorCompat(path);I like this. It’s short and fairly readable.
Imagine trying to create this same interpolator by explicitly implementing getInterpolation for a general odd $n$. I’d wager that (a) computing the appropriate expression(s) would take you a while, and (b) the resulting algebraic representation could either be compact, or readable, but not both.
What Next?
Go forth and explore Path-based interpolators. Hopefully this introduction has given you some inspiration. There are definitely many areas to investigate still, including:
-
how interpolated values are actually calculated when using a
Path-based interpolator; -
whether or not numerical/tabular representations of interpolators exist/are useful;
-
methods for generating more practical
Path-based interpolators.
Further Reading
The Android framework has some interesting internal interpolators. For a more complex algebraic interpolator based on fluid physics, check out ViscousFluidInterpolator, an inner class of android.widget.Scroller used to animate flings.