More On Android Pie’s Brightness Control Changes

This post expands on TJ’s excellent article describing how the brightness control changes in Android Pie practically affect Android developers. Let’s get nerdier in a quest to understand more about this new behavior.

The brightness control change we’re interested in was motivated and described in an Android Developers Blog post as follows:

Humans perceive brightness on a logarithmic rather than linear scale. That means changes in screen brightness are much more noticeable when the screen is dark versus bright. To match this difference in perception, we updated the brightness slider UI in the notification shade and System Settings app to work on a more human-like scale.

Controls that operate on relatable, “human-like” scales usually lead to simpler mental models and more intuitive user experiences, so this is a great decision! Unfortunately, it made TJ’s life as a developer a little more tricky. In order to keep his brightness-control app DigiLux functioning how users expected, he needed to reverse-engineer the newly-introduced nonlinear relationship between slider input values and display brightness setting values. This reverse engineering was made difficult by two key factors:

1. Human perception of brightness is not perfectly logarithmic (and therefore, neither are most brightness transformation functions);
2. Android’s slider input values and display brightness setting values are both discretized (represented by integers in the range 0…255).

Factor 1 explains why TJ’s logarithmic best-fit curve did not perfectly match the data points he measured. In particular, we can see that the curve does not pass through (0, 0) (arrow 1), deviates noticeably from measured values in some regions (arrow 2), and fails to capture a strange flat section of measured values (arrow 3):

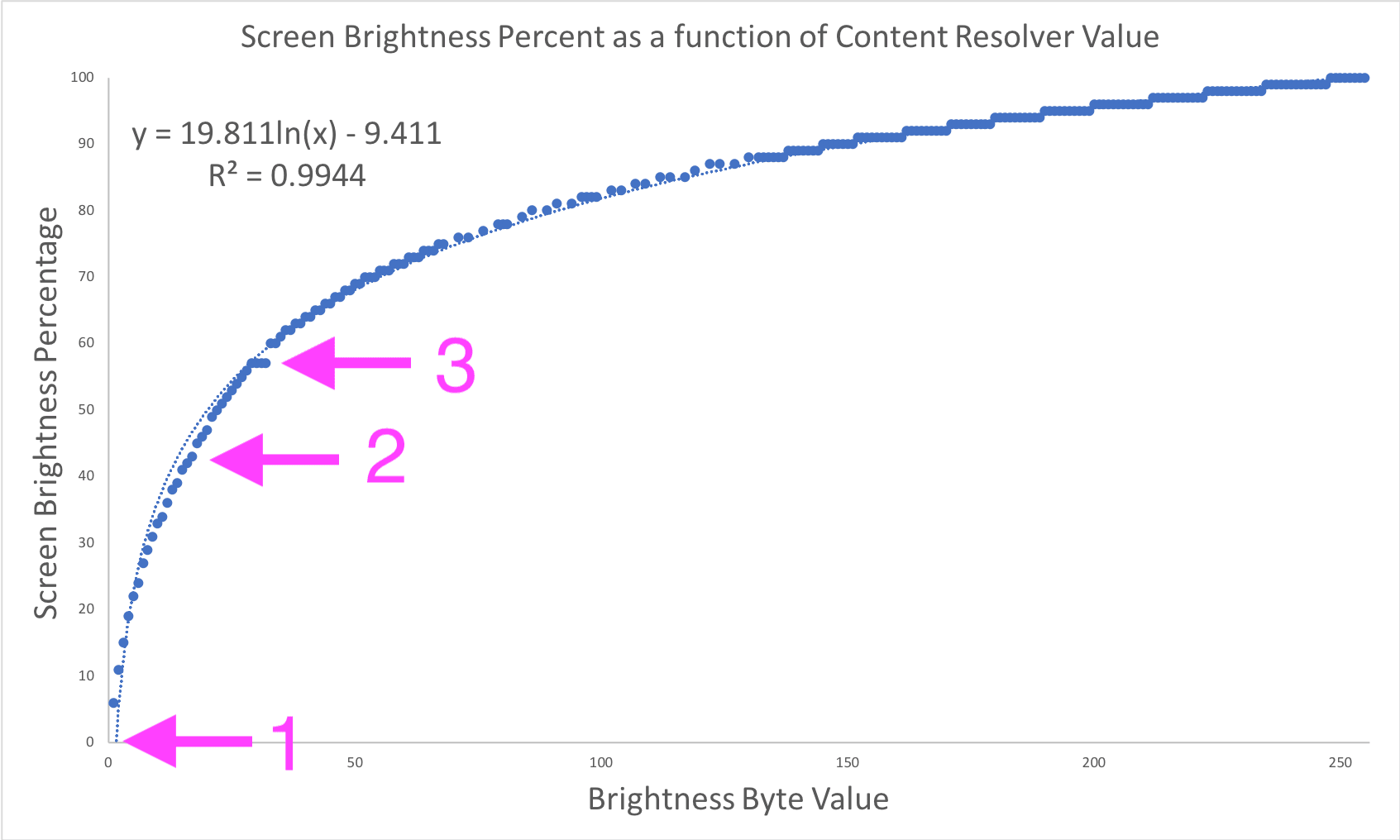
After this analytic approach failed to produce the required accuracy, TJ wisely decided to use his measurements to create a simple and efficient lookup table to perform transformations. Problem solved; job done; app updated; users happy!

Now’s where we get extra nerdy.

Android’s brightness slider is part of the system UI, which means its source code lives in AOSP. The slider is defined in the BrightnessController class. This class implements an onChanged method to process changes in the brightness slider’s value. I’ve highlighted the important lines below:

@Override
public void onChanged(ToggleSlider toggleSlider, boolean tracking, boolean automatic,
        int value, boolean stopTracking) {
    
    // ...

    final int val = convertGammaToLinear(value, min, max);
    setBrightness(val);

    // ...
}

Jackpot! The function convertGammaToLinear and its inverse, convertLinearToGamma, represent the nonlinear mappings TJ reverse-engineered. These functions are defined in the BrightnessUtils class, so we can now see exactly how they are implemented by the platform:

public static final int GAMMA_SPACE_MAX = 1023;

// Hybrid Log Gamma constant values
private static final float R = 0.5f;
private static final float A = 0.17883277f;
private static final float B = 0.28466892f;
private static final float C = 0.55991073f;

public static final int convertGammaToLinear(int val, int min, int max) {
    final float normalizedVal = MathUtils.norm(0, GAMMA_SPACE_MAX, val);
    final float ret;
    if (normalizedVal <= R) {
        ret = MathUtils.sq(normalizedVal / R);
    } else {
        ret = MathUtils.exp((normalizedVal - C) / A) + B;
    }
    // HLG is normalized to the range [0, 12], so we need to re-normalize to the range [0, 1]
    // in order to derive the correct setting value.
    return Math.round(MathUtils.lerp(min, max, ret / 12));
}

public static final int convertLinearToGamma(int val, int min, int max) {
    // For some reason, HLG normalizes to the range [0, 12] rather than [0, 1]
    final float normalizedVal = MathUtils.norm(min, max, val) * 12;
    final float ret;
    if (normalizedVal <= 1f) {
        ret = MathUtils.sqrt(normalizedVal) * R;
    } else {
        ret = A * MathUtils.log(normalizedVal - B) + C;
    }
    return Math.round(MathUtils.lerp(0, GAMMA_SPACE_MAX, ret));
}

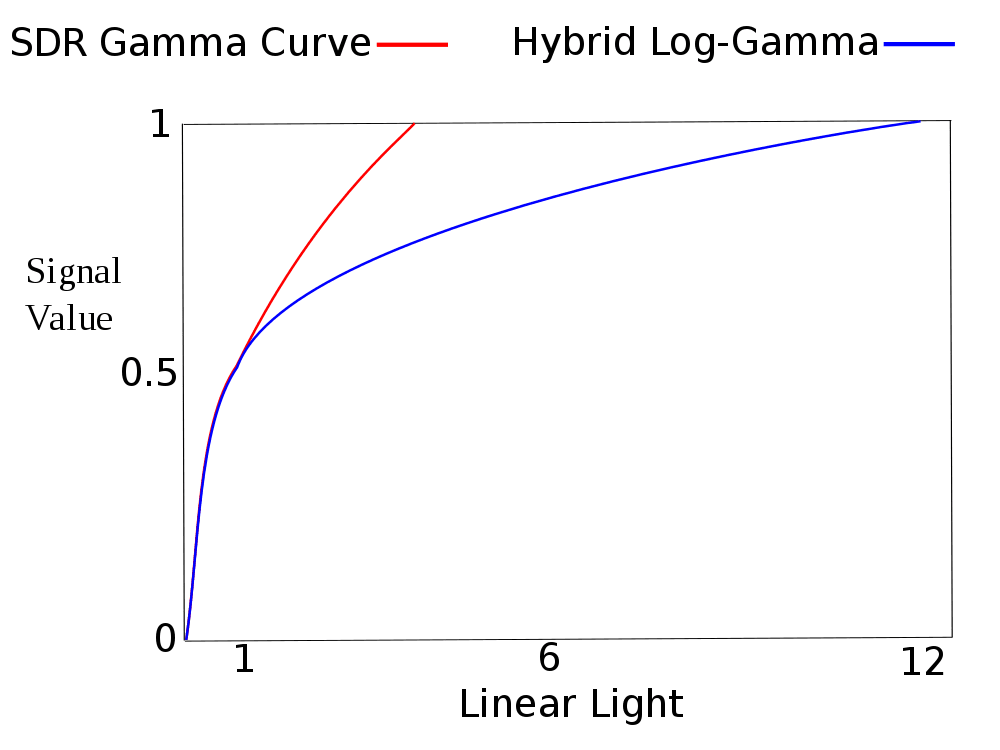
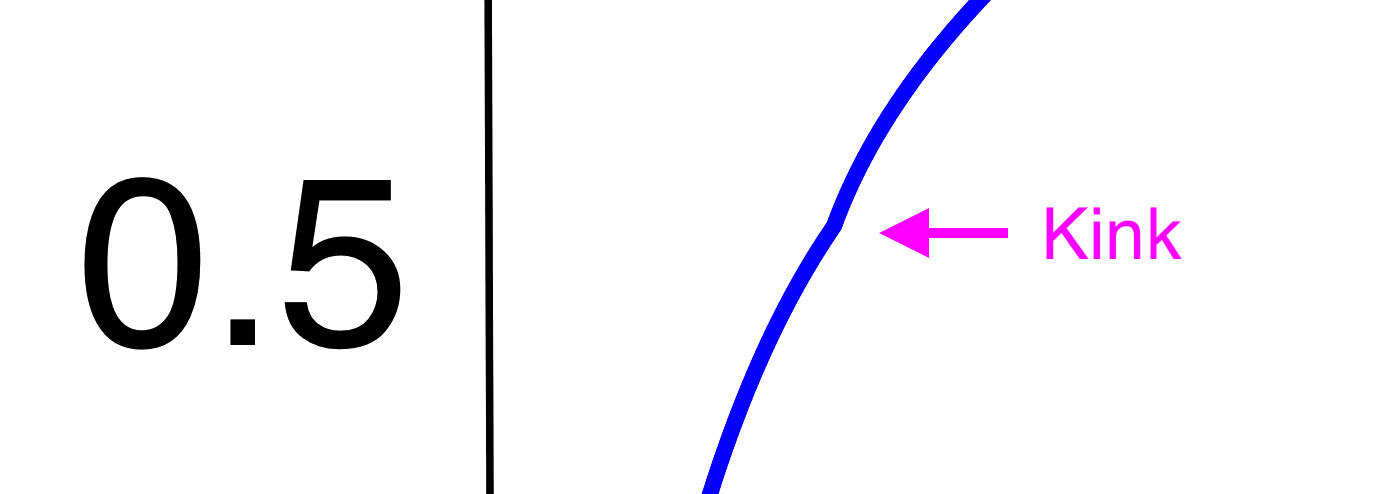
The inline comments indicate that these functions are derived from the Hybrid Log-Gamma transformation. This transformation patches together a gamma-curve (yes, that gamma) and a logarithmic curve to approximate actual human brightness perception. The blue curve below represents this transformation. Note that it passes through (0, 0) and has a small kink at output value 0.5 (magnified in the second image for clarity), just like TJ’s experimental measurements. Now we know where that kink comes from!